The mathematical secrets of Pascal’s triangle - Wajdi Mohamed Ratemi

Pascal's triangle is a number triangle with numbers arranged in staggered rows such that

(1)

where 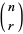 is a binomial coefficient. The triangle was studied by B. Pascal, although it had been described centuries earlier by Chinese mathematician Yanghui (about 500 years earlier, in fact) and the Persian astronomer-poet Omar Khayyám. It is therefore known as the Yanghui triangle in China.

Starting with 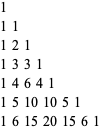, the triangle is

(2)

(OEIS A007318). Pascal's formula shows that each subsequent row is obtained by adding the two entries diagonally above,

(3)

The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Pascal's triangle.

The first number after the 1 in each row divides all other numbers in that row iff it is a prime.

The sums 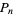 of the number of odd entries in the first  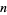rows of Pascal's triangle for 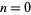, 1, ... are 0, 1, 3, 5, 9, 11, 15, 19, 27, 29, 33, 37, 45, 49, ... (OEIS A006046). It is then true that

(4)

(Harborth 1976, Le Lionnais 1983), with equality for 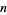 a power of 2, and the power of  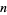given by the constant

(5)

(OEIS A020857). The sequence of cumulative counts of odd entries has some amazing properties, and the minimum possible value 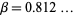(OEIS A077464) is known as the Stolarsky-Harborth constant.

Pascal's triangle contains the figurate numbers along its diagonals, as can be seen from the identity

			(6)
			(7)

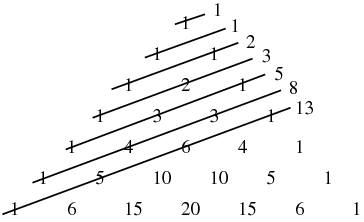
In addition, the sum of the elements of the 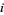th row is

(8)

so the sum of the first  rows (i.e., rows 0 to ) is the Mersenne number

(9)

The "shallow diagonals" of Pascal's triangle sum to Fibonacci numbers, i.e.,

			(10)
			(11)
			(12)
			(13)
			(14)
			(15)

and, in general,

(16)

The numbers of times that the numbers 2, 3, 4, ... occur in Pascal's triangle are given by 1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... (OEIS A003016; Ogilvy 1972, p. 96; Comtet 1974, p. 93; Singmaster 1971). Similarly, the numbers of rows in which the numbers 2, 3, 4, ... occur are 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 2, ... (OEIS A059233).

By row 210, the numbers

			(17)
			(18)
			(19)

have appeared six times, more than any other number (excluding 1). By row 1540,

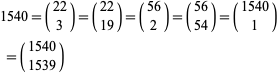(20)

has now occurred six times, by row 3003,

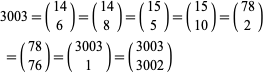(21)

has now occurred 8 times, and by row 7140, 7140 has appeared six times as well. In fact, the numbers that occur five or more times in Pascal's triangle are 1, 120, 210, 1540, 3003, 7140, 11628, 24310, ... (OEIS A003015), with no others up to .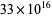

It is known that there are infinitely many numbers that occur at least 6 times in Pascal's triangle, namely the solutions to

(22)

given by

			(23)
			(24)

where 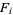 is the 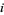th Fibonacci number (Singmaster 1975). The first few such values of  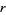for , 2, ... are 1, 3003, 61218182743304701891431482520, ... (OEIS A090162).

There is an unexpected connection between Pascal's triangle and the Delannoy numbers via Cholesky decomposition (G. Helms, pers. comm., Aug. 29, 2005). What's more, despite the two being mathematically unrelated, there's also a topical connection between Pascal's triangle and the so-called rascal triangle; this relationship also provides a tangential relation to the cake cutting problem and hence to the cake numbers.

Pascal's triangle (mod 2) turns out to be equivalent to the Sierpiński sieve (Wolfram 1984; Crandall and Pomerance 2001; Borwein and Bailey 2003, pp. 46-47). Guy (1990) gives several other unexpected properties of Pascal's triangle.

SEE ALSO:Bell Triangle, Bernoulli Triangle, Binomial Coefficient, Binomial Theorem, Brianchon's Theorem, Cake Cutting, Catalan's Triangle, Christmas Stocking Theorem, Clark's Triangle, Cylinder Cutting, Euler's Number Triangle, Fibonacci Number, Figurate Number Triangle, Leibniz Harmonic Triangle,Losanitsch's Triangle, Number Triangle, Pascal's Formula, Pascal Matrix, Polygon, Rascal Triangle, Seidel-Entringer-Arnold Triangle, Sierpiński Sieve, Space Division by Planes, Square Division by Lines, Star of David Theorem, Stolarsky-Harborth Constant, Trinomial TrianglePortions of this entry contributed by Christopher Stover